Topic 1 Fractions

A fraction is a part of a whole. In arithmetic, and more broadly in mathematics, it is expressed as the division of two numbers, e.g. \(\frac{1}{2}\) can be read as “one out of two”, \(\frac{3}{4}\) can be read as “3 out of four.”

These fractions can be represented graphically with coloured squares or rectangles

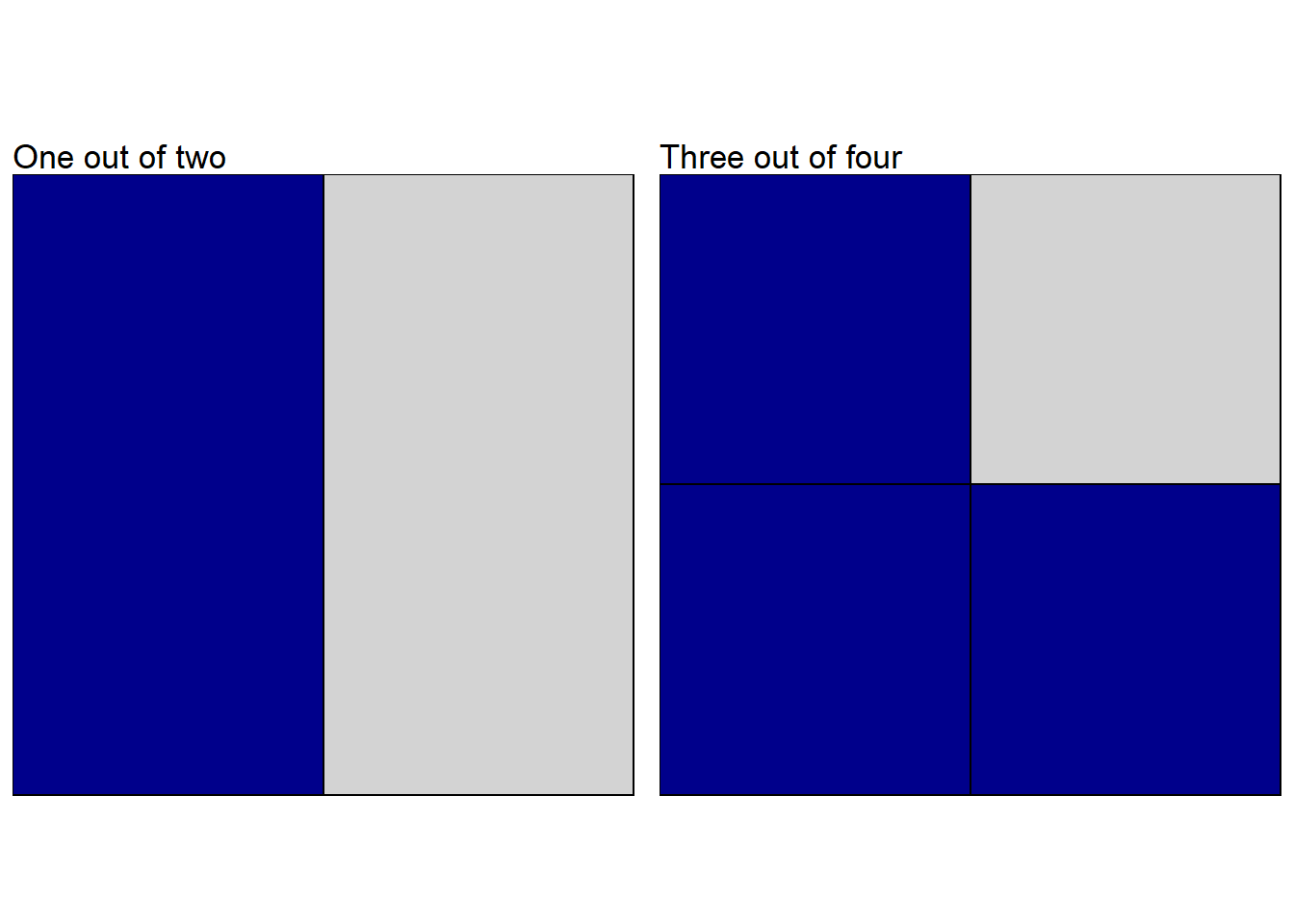
One out of two and three out of four

Figure 1.1: One out of two and three out of four

Of course for these fractions you are more likely to say “half” or “three quarters,” similarly \(\frac{7}{312}\) can be said”seven three-hundred-and-twelfths” or “7 out of 312.”1

In order to make talking about fractions easier, you ought to be aware of a bit of terminology. The top of the fraction is referred to as the numerator and the bottom as the denominator; e.g. with \(3/4\) the numerator is \(3\) and the denominator is \(4\).

1.1 Equivalent fractions

One out of two (\(1 \over 2\)) is the same as two out of four (\(2 \over 4\)) or three out of six (\(3 \over 6\)) — in all three cases half of the square is filled.

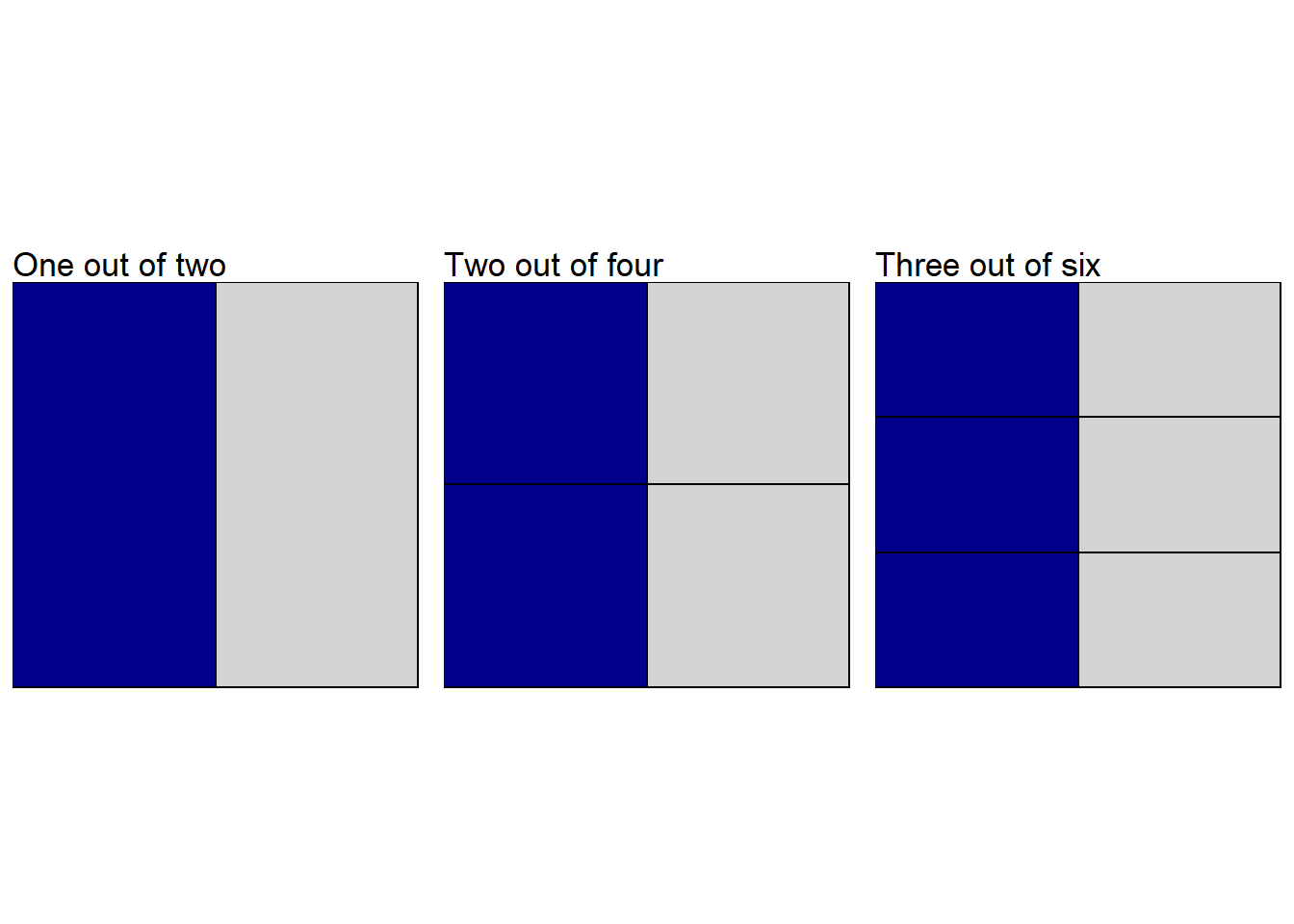
One out of two, two out of four and three out of six

Figure 1.2: One out of two, two out of four and three out of six

These are referred to as equivalent fractions. If you compare \(\frac{1}{2}\),\(\frac{2}{4}\) and \(\frac{3}{6}\) you can see that you can move from one to the other by multiplying both the numerator (the top) and the denominator (the bottom) by the same number. What you are basically doing is splitting the square up into smaller and smaller bits, but you still have the same amount of the square coloured in.

Normally you write a fraction in its “simplest form,” which is when there are no common factors between the numerator and denominator — i.e. there is no number you can divide both top and bottom by leaving both as whole numbers.

E.g.

  • In \(\frac{2}{4}\) both top and bottom can be divided by \(2\), leaving \(\frac{1}{2}\).
  • In $\(\frac{6}{15}\) both the top and bottom are multiples of \(3\) so we can divide them both by that and end up with \(\frac{2}{5}\).

TEST: Simplest form

1.2 Multiplying fractions

If I want to find out what half of one third is, I need to multiply the fractions.

Graphically one third is

One third

Figure 1.3: One third

So to calculate half of this, I split each of my rectangles into two,

Two sixths

Figure 1.4: Two sixths

which is the equivalent fraction \(\frac{2}{6}\) and then I get rid of half of the shaded rectangles

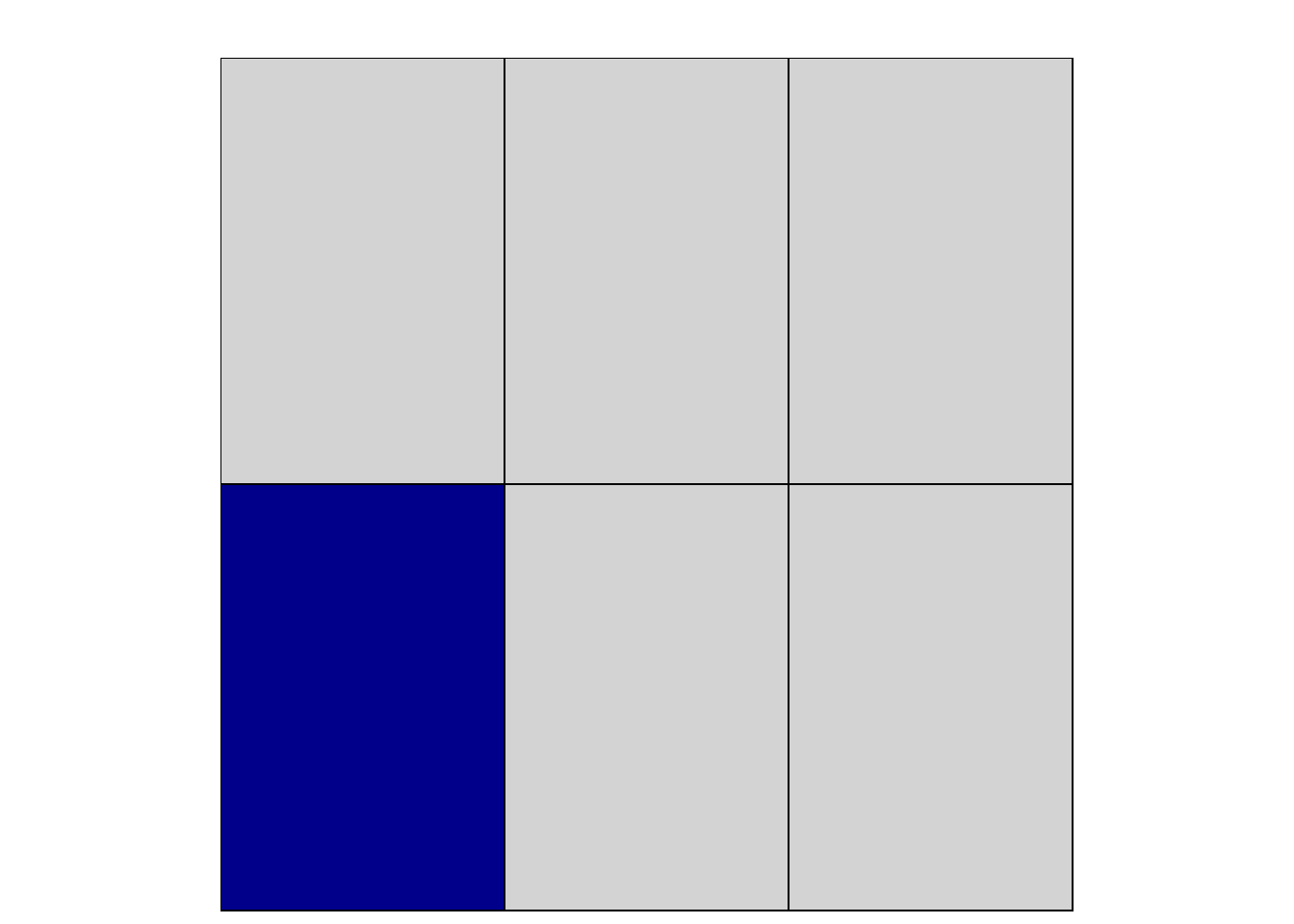
One sixths

Figure 1.5: One sixths

leaving only one of the six rectangles shaded, i.e. I have \(\frac{1}{6}\). So we found

\[\frac{1}{2} \times \frac{1}{3} = \frac{1}{6}\]

If you look at the numbers carefully, you may see that we could have come to the same answer by multiplying the numerators, and multiplying the denominators

\[\begin{align} \frac{1}{2} \times \frac{1}{3} &= \frac{1 \times 1}{2 \times 3}\\ &= \frac{1}{6} \end{align}\]

Similarly if we wanted to multiply \(\frac{3}{5}\) and \(\frac{2}{7}\) we would do

\[\begin{align} \frac{3}{5} \times \frac{2}{7} &= \frac{3 \times 2}{5 \times 7}\\ &= \frac{6}{35} \end{align}\]

Of course we normally want to express the fractions in their simplest form, which can be done in two ways: firstly you can multiply the fractions as above, and then find the simplest form by looking for common factors, as you did in the section on equivalent fractions. This will always work, but may lead to large numbers (which isn’t a problem if you’re using a calculator). Another way is to look for common factors before completing the multiplications. E.g.

\[\frac{2}{3} \times \frac{1}{4} = \frac{2 \times 1}{3 \times 4}\] If I look at the fraction on the right hand side, I can see that I have a \(2\) on the top, and a \(4\) on the bottom, so I can divide both top and bottom by \(2\), giving

\[ \frac{2 \times 1}{3 \times 4} = \frac{1 \times 1}{3 \times 2}\] leading to \(\frac{1}{6}\). I.e.

\[\begin{align} \frac{2}{3} \times \frac{1}{4} &= \frac{2 \times 1}{3 \times 4}\\ &= \frac{1 \times 1}{3 \times 2}\\ &= \frac{1}{6} \end{align}\]

TEST: Multiply and simplest form

1.3 Adding and subtracting fractions

One of the most common things you will do with fractions is to add them. Let’s look graphically at \(\frac{1}{2}\) and \(\frac{1}{3}\).

A half and a third

Figure 1.6: A half and a third

As it stands, it’s not at all obvious how to add them, however if I split my square up into sixths instead, I get \(\frac{3}{6}\) and \(\frac{2}{6}\) as my equivalent fractions.

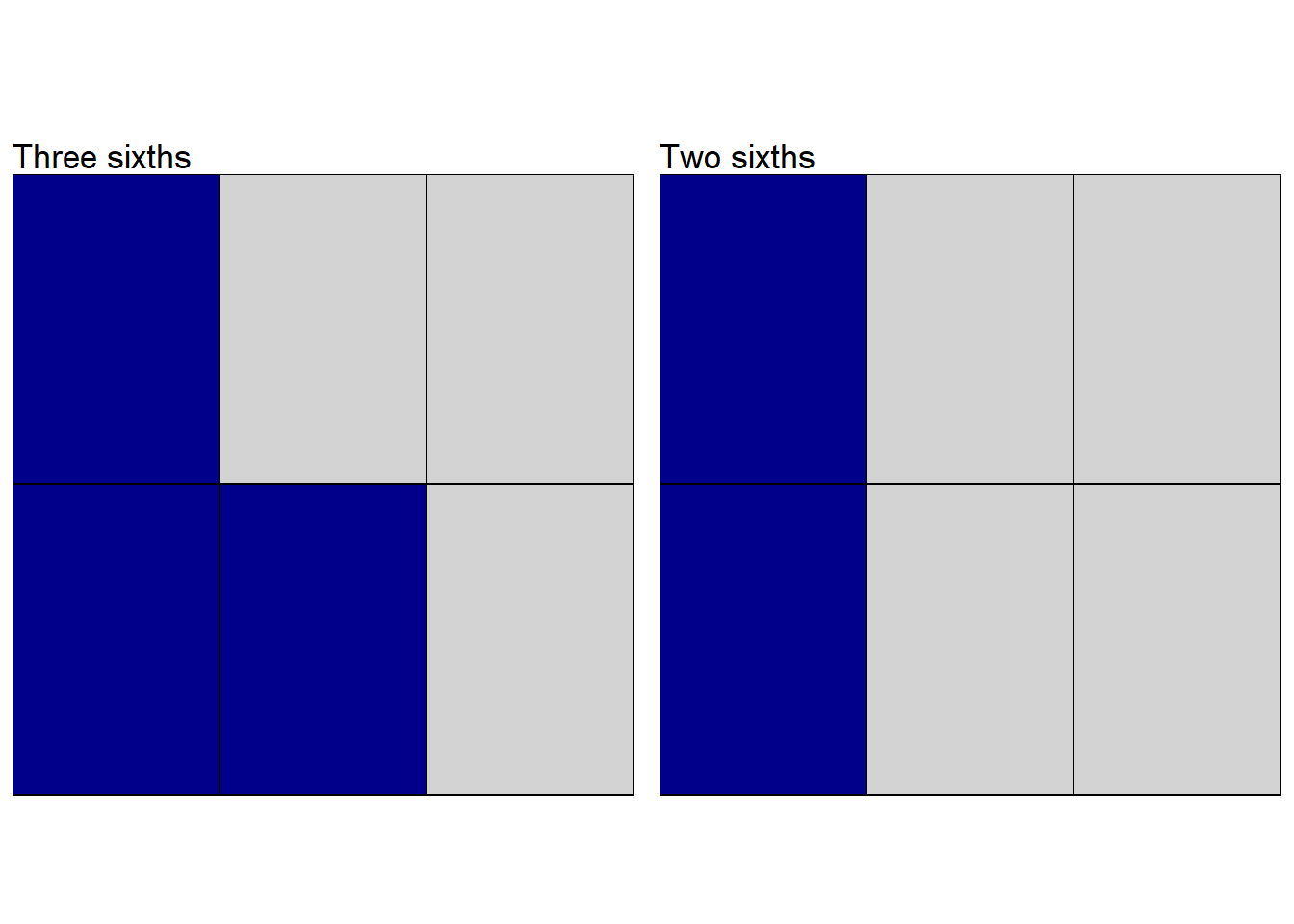
Three sixths and two sixths

Figure 1.7: Three sixths and two sixths

and it is then easier to see that if I add the two fractions I get \(\frac{5}{6}\).

Five sixths

Figure 1.8: Five sixths

I.e.

\[\begin{align} \frac{1}{2} + \frac{1}{3} &= \frac{3}{6} + \frac{2}{6} \\ &= \frac{3 + 2}{6}\\ &= \frac{5}{6} \end{align}\]

This illustrates the standard way to add fractions.

  1. Find a common denominator
    • This is a number which is a multiple of both denominators
    • The best one is the least common multiple of the two numbers, but if you can’t find that any multiple will do, and you can cancel down to the simplest form later.
  2. Convert both fractions to their equivalents with that common denominator.
  3. Add the numerators.

E.g. Adding \(\frac{1}{2}\) to \(\frac{1}{4}\)

  1. The denominators are \(2\) and \(4\), so a good common denominator is \(4\) as both go into it.
  2. I don’t need to change the \(\frac{1}{4}\) as it already has this denominator, but I have to change the \(\frac{1}{2}\) into the equivalent fraction \(\frac{2}{4}\).
  3. I now have both fractions over the same denominator, so can add the fractions \[\begin{align} \frac{1}{2} + \frac{1}{4} &= \frac{2}{4} + \frac{1}{4} \\ &= \frac{2 + 1}{4}\\ &= \frac{3}{4} \end{align}\]

E.g. Adding \(\frac{1}{3}\) to \(\frac{1}{8}\)

  1. The denominators are \(3\) and \(8\); no number goes into both, so the smallest number both go into is \(3 \times 8 = 24\), so a good common denominator is \(24\).
  2. \(\frac{1}{3}\) is equivalent to $, and \(\frac{1}{8}\) is equivalent to \(\frac{3}{24}\)
  3. I now have both fractions over the same denominator, so can add the fractions \[\begin{align} \frac{1}{3} + \frac{1}{8} &= \frac{8}{24} + \frac{3}{24} \\ &= \frac{8 + 3}{24}\\ &= \frac{11}{24} \end{align}\]

E.g. Adding \(\frac{1}{6}\) to \(\frac{1}{9}\)

  1. The denominators are \(6\) and \(9\); the smallest number both go into is \(18\) (it is \(3 \times 6\) and \(2 \times 9\)), so this makes a good common denominator.
  2. \(\frac{1}{6}\) is equivalent to $, and \(\frac{1}{9}\) is equivalent to \(\frac{2}{18}\)
  3. I now have both fractions over the same denominator, so can add the fractions \[\begin{align} \frac{1}{6} + \frac{1}{9} &= \frac{3}{18} + \frac{2}{18} \\ &= \frac{3 + 2}{18}\\ &= \frac{5}{18} \end{align}\]

Subtracting fractions works the same way. e.g. \[\begin{align} \frac{1}{6} - \frac{1}{9} &= \frac{3}{18} - \frac{2}{18} \\ &= \frac{3 - 2}{18}\\ &= \frac{1}{18} \end{align}\]

1.4 Improper fractions and mixed numbers

There is nothing to stop the numerator of a fraction being bigger than the denominator — e.g. if you have two and a half chocolate bars, you can also think of this as five halves. Fractions which are top-heavy in this way are referred to as improper fractions, but, despite the name, there’s nothing wrong with them.

For most calculation purposes it is useful to leave fractions as improper, however when presenting final results to people it is conventional to convert the fraction into a mixed number, consisting of how many whole parts you have, and then the fractional part left over.

E.g. \(\frac{5}{2}\) is an improper fraction. The denominator \(2\) goes into the numerator \(5\) twice, with remainder \(1\), so we have two wholes and a half left over, which we would write as \(2\frac{1}{2}\)

You could look at this symbolically as \[\begin{align} \frac{5}{2} &= \frac{4+1}{2}\\ &= \frac{4}{2} + \frac{1}{2}\\ &= 2 + \frac{1}{2}\\ &= 2\frac{1}{2} \end{align}\]

1.5 Dividing by fractions

Before diving into division by fractions, I need to introduce the concept of the reciprocal. The reciprocal is just one divided by the number. E.g.

  • the reciprocal of \(2\) is \(\frac{1}{2}\)
  • the reciprocal of \(4\) is \(\frac{1}{4}\)

Another way to look at this is to notice that \(2\) is the same as the fraction \(\frac{2}{1}\). This is obviously not how you would normally write it, but is perfectly valid. Now the previous two statements about reciprocals can be written as

  • the reciprocal of \(\frac{2}{1}\) is \(\frac{1}{2}\)
  • the reciprocal of \(\frac{4}{1}\) is \(\frac{1}{4}\)

I.e. you can think of finding the reciprocal as flipping the fraction over. This then generalises nicely to reciprocals of fractions

  • the reciprocal of \(\frac{1}{2}\) is \(\frac{2}{1}\), i.e. \(2\)
  • the reciprocal of \(\frac{1}{4}\) is \(\frac{4}{1}\), i.e. \(4\)
  • the reciprocal of \(\frac{3}{4}\) is \(\frac{4}{3}\)
  • the reciprocal of \(\frac{4}{3}\) is \(\frac{3}{4}\)
  • the reciprocal of \(\frac{2}{5}\) is \(\frac{5}{2}\)
  • the reciprocal of \(\frac{5}{2}\) is \(\frac{2}{5}\)

This now brings us on to dividing by fractions. The key is to realise that dividing by something is the same as multiplying by the reciprocal.

E.g.

  • \[\begin{align} 6 \div 2 &= 6 \times \frac{1}{2}\\ &= 3 \end{align}\]
  • \[\begin{align} 12 \div 3 &= 12 \times \frac{1}{3}\\ &= 4 \end{align}\]

This is just as true if the divisor is a fraction as if it’s an integer

E.g.

  • \[\begin{align} 3 \div \frac{1}{2} &= 3 \times \frac{2}{1}\\ &= 3 \times 2\\ &= 6 \end{align}\]
  • \[\begin{align} 4 \div \frac{1}{3} &= 4 \times \frac{3}{1}\\ &= 4 \times 3\\ &= 12 \end{align}\]
  • \[\begin{align} 3 \div \frac{2}{5} &= 3 \times \frac{5}{2}\\ &= \frac{3}{1} \times \frac{5}{2}\\ &= \frac{3 \times 5}{1 \times 2}\\ &= \frac{15}{2} \end{align}\]
  • \[\begin{align} \frac{3}{7} \div \frac{2}{5} &= \frac{3}{7} \times \frac{5}{2}\\ &= \frac{3 \times 5}{7 \times 2}\\ &= \frac{15}{14} \end{align}\]

1.6 Connection to decimals

Every fraction can be represented as a decimal. \(\frac{1}{2}\) means precisely the same thing as \(1 \div 2\). In general you rarely see the symbol \(\div\) used in practice — divisions are almost always expressed as \(\frac{a}{b}\). This means you can convert a fraction to a decimal just by doing the division, either by hand or on a calculator.

One caveat is that a fraction like \(\frac{1}{3}\) leads to an infinitely long decimal representation \(0.33333...\), so you would need to round the number at some point, whereas the fraction representation is exact.

  1. You may also hear people say “7 over 312” which is literally reading the symbols, and is sometimes more convenient when algebra is involved.↩︎