Topic 8 Trigonometry

8.1 Triangles

If you have three pieces of information about a triangle, you can, in all but one case, use either the sine or cosine rule to deduce the missing information. The cases are:

Three sides — use the cosine rule.
Two sides and an angle

If the angle is opposite one of the sides — use the sine rule
If the angle is between the two sides — use the cosine rule

Two angles and a side

Deduce the third angle by the sum of the angles is \(180^{\circ}\) and use the sine rule for the lengths.

Three angles — you need more information to get side lengths; once you have one you can use the sine rule to get the rest.

8.1.1 The sine rule

There are several relationships between the sizes of angles and sides in triangles. The sine rule states that

Triangle with edges and vertices labelled

\[ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\]

Where A, B, and C are the angles at each vertex of the triangle, and a, b and c are the lengths of the sides opposite each angle.

In practice this means that if you have a side and the angle opposite it, and any other angle or side length, you can find the others.

E.g. if \(A = 20^{\circ}\), \(a=2\) and \(b = 3\) we have

\[ \frac{\sin 20^{\circ}}{2} = \frac{\sin B}{3}\] which can be rearranged to give

\[ \sin B = \frac{3\sin 20^{\circ}}{2}\] i.e.

\[ B = \sin^{-1}\left(\frac{3\sin 20^{\circ}}{2}\right)\]

giving \(B = 30.9^{\circ}\).

If you have E.g. if \(A = 20^{\circ}\), \(a=2\) and \(B = 50\) we have

\[ \frac{\sin 20^{\circ}}{2} = \frac{\sin 50^{\circ}}{b}\]

giving

\[ b = \frac{2\sin 50^{\circ}}{\sin 20^{\circ}}\]

So \(b = 4.5\).

8.1.2 The cosine rule

\[a^2 = b^2 + c^2 - 2bc\cos A\] This is useful when you know two sides and the angle between them, or all three sides.

E.g. \(b = 3\), \(c = 4\), \(A = 30^{\circ}\)

Triangle with one angle and two sides

Using the cosine rule gives

\[a^2 = 3^2 + 4^2 - 2\times 3 \times 4 \times \cos 30\] giving \(a^2 = 4.22\), so \(a = 2.1\).

If you know all three sides, and need to know an angle, the equation can be rearranged (or put the numbers in first and the make \(\cos A\) the subject).

\[\cos A = \frac{b^2 + c^2 - a^2}{2bc}\]

E.g. if \(a = 3\), \(b = 4\) and \(c = 5\), we get

\[\cos A = \frac{4^2 + 5^2 - 3^2}{2\times 4 \times 5}\]

giving

\[\cos A = \frac{4}{5}\]

and so \(A = 36.9^{\circ}\).

8.2 Trigonometric equations

If you plug a value of sine, cosine or tangent into your calculator and use the inverse trigonometric functions (\(\sin^{-1}\), \(\cos^{-1}\), \(\tan^{-1}\)) it will give you an angle, which is great, but all these functions repeat every \(360^{\circ}\), so you could add or subrtract 360 to each of these angles, and take its sine, cosine or tangent, and get the same answer.

E.g. \(\sin^{-1}(0.5) = 30^{\circ}\), and so \(\sin(30) = 0.5\), but also \(\sin(390) = 0.5\) and \(\sin(-330) = 0.5\).

Worse still, if you look at a graph of sine, and see where it is 0.5, there are two values even just between 0 and 360 degrees — \(30^{\circ}\) and \(150^{\circ}\).

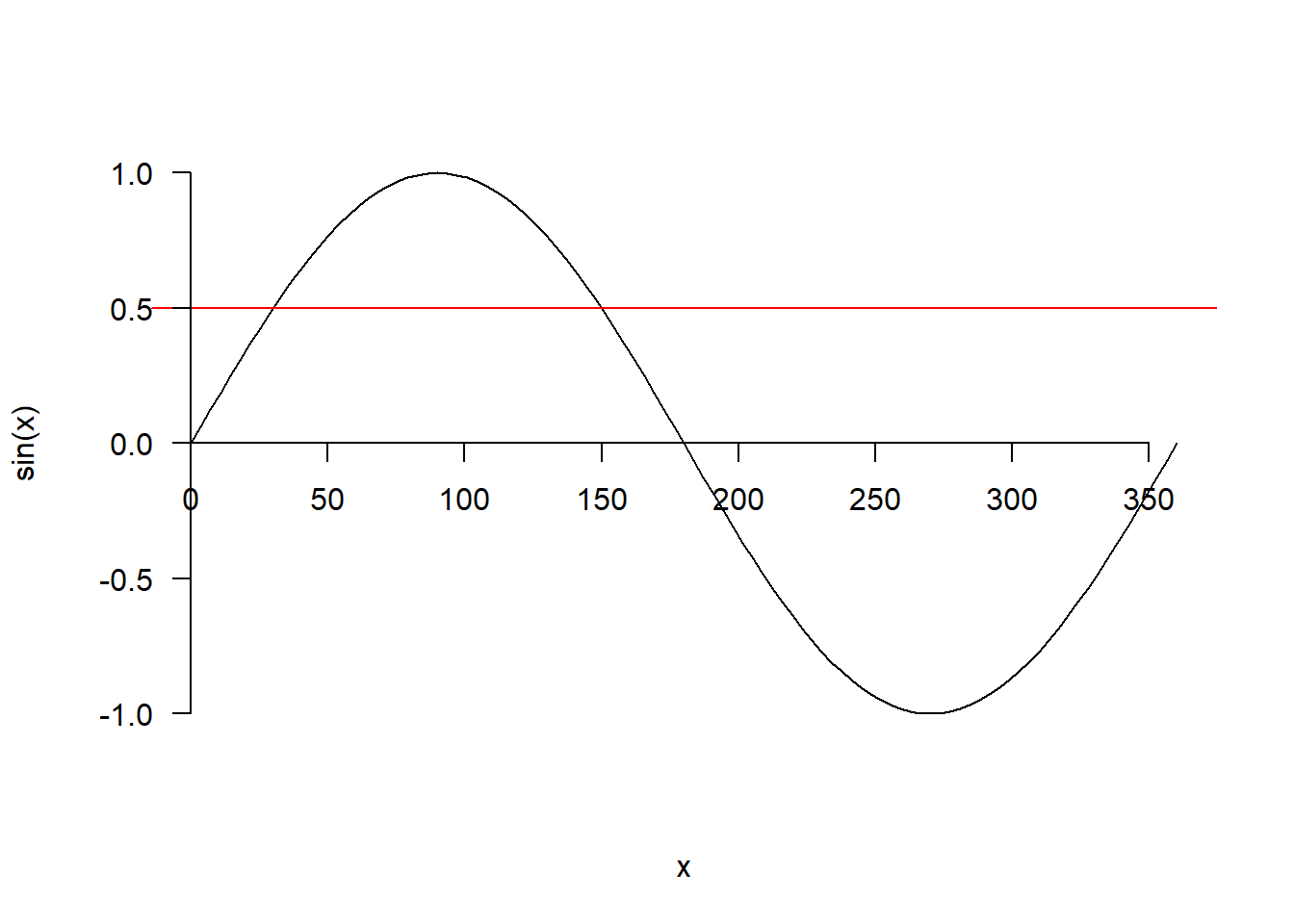
The same goes for the cosine and tangent functions.

This means that if you use the inverse sine, cosine or tangent functions (you will also see these referred to as arcsin, arccos and arctan in many places), your calculator will only give you one of an infinite number of possible values. If you want all the values you need to:

Work out the possible values between \(0^{\circ}\) and \(360^{\circ}\).
Add or subtract \(360^{\circ}\) to your heart’s content to generate other possible angles.
Decide which angles are relevant to your problem.

Step 1 is the hardest, but is made easier by examining the graphs of the functions, and understanding their symmetries.

Looking at the graph carefully you can see some information. The graph splits into four distinct sections, which are called quadrants: quadrant 1 goes from \(0^{\circ}\)–\(90^{\circ}\); quadrant 2 goes from \(90^{\circ}\)–\(180^{\circ}\); quadrant 3 goes from \(180^{\circ}\)–\(270^{\circ}\); and quadrant 4 goes from \(270^{\circ}\)–\(360^{\circ}\).

Quadrant	Angles	Notes
1	\(0^{\circ}\)–\(90^{\circ}\)	All three functions are positive
2	\(90^{\circ}\)–\(180^{\circ}\)	Sin is positive, everything else is negative
3	\(180^{\circ}\)–\(270^{\circ}\)	Tan is positive, everything else is negative
4	\(270^{\circ}\)–\(360^{\circ}\)	Cos is positive, everything else is negative

The patterns of positives go: All, Sin, Cos, Tan. One mnemonic for this is “All Stations Through Crewe,” though most schools these days seem to start in the fourth quadrant and refer to “CAST.”

If you look at the symmetries, you can see (with a bit of work) that, if \(\theta\) is an angle in the first quadrant, the sine, cosine or tangent will be equal, apart from the sign to the sine, cosine or tangent of \(180-\theta\) in the second quadrant, \(180+\theta\) in the third quadrant, and \(360-\theta\) in the fourth quadrant.

This suggests one possible strategy if you have a sin, cosine or tangent and want to work out all the angles:

If you are given a value x for sine, cosine or tangent

Look at the sign of x and work out which quadrants you are interested in:

function	positive	negative
\(\sin\)	1 and 2	3 and 4
\(\cos\)	1 and 4	2 and 3
\(\tan\)	1 and 3	2 and 4

Ignore the sign of x and use the \(\sin^{-1}\), \(\cos^{-1}\) or \(\tan^{-1}\) function on your calculator (or use exact values if you can remember them) to find out the first quadrant angle \(\theta\) — note that this is not necessarily one of your solutions.
Use \(\theta\) calculated to find your two solutions between \(0^{\circ}\) and \(360^{\circ}\), depending on which quadrants you are interested in:

quadrant	angle
1	\(\theta\)
2	\(180 - \theta\)
3	\(180 + \theta\)
4	\(360 - \theta\)

E.g. If I am told \(\sin A = -0.5\)

This is \(\sin\) and is negative, so I’m interested in the third and fourth quadrants
Ignoring the sign tells me the first quadrant angle would be \(30^{\circ}\).
I am looking at third and fourth quadrants, so my solutions are \(A = 180 + 30\) for the third quadrant, and \(A = 360 - 30\) for the fourth quadrant. I.e. \(A = 210^{\circ}\) and \(A = 330^{\circ}\)

You may have been taught a different strategy, but all ways give the same results.

8.3 The addition formulas

There are various formulae which can be used when you are using trigonometric functions of sums or differences of angles. The most basic are:

\[\begin{align} \cos(A + B) &= \cos(A)\cos(B) - \sin(A)\sin(B)\\ \cos(A - B) &= \cos(A)\cos(B) + \sin(A)\sin(B)\\ \sin(A + B) &= \sin(A)\cos(B) + \cos(A)\sin(B)\\ \sin(A - B) &= \sin(A)\cos(B) - \cos(A)\sin(B) \end{align}\]

From which, using \(\tan(A) = \frac{\sin(A)}{\cos(A)}\), one can derive

\[\begin{align} \tan(A + B) &= \frac{\tan(A) + \tan(B)}{1-\tan(A)\tan(B)}\\ \tan(A - B) &= \frac{\tan(A) - \tan(B)}{1+\tan(A)\tan(B)} \end{align}\]

Two very important ones, which follow from these, are the double angle formulae for sine and cosine

\[\begin{align} \cos(2A) &= \cos^2(A) - \sin^2(A)\\ \sin(2A) &= 2\sin(A)\cos(A) \end{align}\]

There is also a double angle one for tangent too

\[\tan(2A) = \frac{2\tan(A)}{1-\tan^2(A)}\]

8.4 sec, cosec and cot

It is convenient to define the reciprocal trigonometric functions

\[ \sec A = \frac{1}{\cos A}\]

\[ \mathrm{cosec}A = \frac{1}{\sin A}\] \[ \cot A = \frac{1}{\tan A}\]

Most calculators don’t have functions to calculate these, so you will need to use the formulae above.

8.5 Identities

The definition of the tangent function gives us the following relationship:

\[ \tan A = \frac{\sin A}{\cos A}\] and Pythagoras’ Theorem gives

\[ \cos^2 A + \sin^2 A = 1\] from which, by dividing by \(\cos^2 A\) we get

\[ 1 + \tan^2 A = \sec^2 A\]

and dividing by \(sin^2 A\) gives

\[ \cot^2 A + 1 = \mathrm{cosec}^2 A\]

8.6 Harmonic form

It is difficult to analyse an equation such as

\[\begin{equation} y = 3\cos x - 4\sin x \tag{8.1} \end{equation}\]

however the cosine and sine addition formulae give us a way to combine the two terms on the right hand side into one term.

E.g. Suppose we could write equation (8.1) in the form

\[\begin{equation} y = R\cos(x + \alpha) \tag{8.2} \end{equation}\]

what would \(R\) and \(\alpha\) be?

Using the addition formula for cosine on equation (8.2) gives

\[\begin{equation} R\cos(x + \alpha) = R(\cos x\cos\alpha - \sin x\sin\alpha) \tag{8.3} \end{equation}\]

Setting equations (8.3) and (8.1) equal to each other, and swapping the order in each term on the left had side, gives:

\[\begin{equation} R(\cos \alpha\cos x - \sin \alpha\sin x) = 3\cos x - 4\sin x \tag{8.4} \end{equation}\]

from which, if the two sides are to be equal to each other for all values of x, we get

\[\begin{align} R \cos \alpha &= 3\\ R \sin \alpha &= 4 \end{align}\]

Dividing the second of these by the first gives

\[\frac{\sin \alpha}{\cos \alpha} = \frac{4}{3}\] which gives us \(\tan\alpha = \frac{4}{3}\), and so \(\alpha = 53.1^{\circ}\) (we are restricting \(\alpha\) to the first quadrant.)

Squaring each equation and adding gives us:

\[R^2\cos^2\alpha + R^2\sin^2\alpha = 3^2 + 4^2\] Factorising the left side gives

\[R^2(\cos^2\alpha + \sin^2\alpha) = 3^2 + 4^2\]

which, from the trigonometric identity \(\cos^2 A + \sin^2 A = 1\), means

\[R^2 = 3^2 + 4^2\] which gives \(R = 5\).

From this we can conclude that

\[3\cos x - 4\sin x = 5\cos(x - 53.1^{\circ})\]

for all values of x, so

\[y = 5\cos(x - 53.1^{\circ})\]

which now allows us to see where y is a maximum, minimum, or 0 just from our knowledge of the cosine function. This way of writing the sum of two sines or cosines as one function is called harmonic form. Note that it only works if the argument of the trigonometric functions is the same.

Let’s look at the addition formulae again:

These suggest the following:

\(a\cos x - b\sin x \equiv R\cos(x + \alpha)\)
\(a\cos x + b\sin x \equiv R\cos(x - \alpha)\)
\(a\sin x + b\cos x \equiv R\sin(x + \alpha)\)
\(a\sin x - b\cos x \equiv R\sin(x - \alpha)\)

where \(a = R\cos \alpha\) and \(b = R\sin \alpha\), so \(R = \sqrt{a^2 + b^2)}\) and \(\alpha = \tan^{-1}\left(\frac{b}{a}\right)\).

E.g.

\(4\cos x - 5\sin x \equiv \sqrt{41}\cos(x + 51.3^{\circ})\)

8.7 Radians

There are 360 degrees in a full circle. Why 360? It was chosen several thousand years ago by the Babylonians, and there are several theories as to why. Mathematically it is quite a nice number as it can be divided nicely by 2, 3, 4, 5, 6, 8, 10, … which certainly makes it nice if you don’t have a calculator. When all is said and done, though, it is just a number, and any other number could be used, and a different angle measure created.

One unit which is very commonly used in science, mathematics and engineering is the radian. This is defined as the distance travelled around the circle, divided by the radius of the circle. If you go completely around a circle you have travelled a distance \(2\pi r\), there are \(2\pi\) radians in a circle.

More formally, if you measure an arc of length s around a circle of radius r, the angle \(\alpha\) the arc makes is given by

\[\alpha = \frac{s}{r}\]

Radians

E.g. If the arc length is 5 cm, and the radius of the circle is 10cm, the angle is \(\frac{5}{10} = 0.5\) cm.

As stated earlier, \(360^{\circ}\) splits nicely into smaller angles. This doesn’t work so well with radians, unless you leave the radians as multiples of \(\pi\). E.g. half a circle is \(\frac{360}{2} = 180^{\circ}\), but can also be written as \(\frac{2\pi}{2}=\pi\) radians.

Useful angles are:

Fraction of circle	Degrees	Radians
Whole circle	360	\(2\pi\)
Half	180	\(\pi\)
Quarter	90	\(\pi\)
Sixth	60	\(\frac{\pi}{3}\)
Eighth	45	\(\frac{\pi}{4}\)
Twelfth	30	\(\frac{\pi}{6}\)

It is easy to convert angles between radians and degrees. If \(\theta\) is the angle in degrees, and \(\alpha\) is the angle in radians:

\[ \alpha = \frac{\theta\pi}{180} \qquad \theta = \frac{180\alpha}{\pi}\] E.g.

\(20^{\circ}\) is \(\frac{20\times\pi}{180} = \frac{1}{9}\pi\)
5 radians is \(\frac{180\times 5}{\pi} = 286^{\circ}\)

8.7.1 Trigonometry with radians

When using the trigonometric functions it is important to know whether the angles are measured in degrees or radians, and, if you are using a calculator, to set your calculator into the correct mode.

Every trigonometric result is still true in whatever angle unit you use.

8.8 Small angle approximations

When you are using radians as the angle unit, and the angle is very small, there are some very useful approximations:

\[\begin{align} \sin \alpha &\approx \alpha\\ \cos \alpha &\approx 1 - \alpha^2\\ \tan \alpha &\approx \alpha \end{align}\]