Topic 5 Simultaneous equations

Often you will have several variables which are related to each other and several equations describing those relationships.

E.g. two coffees and a tea cost £5, three coffees and five teas cost £11, how much is a coffee and how much is a tea? This can be translated into equations to make the pair of equations in c (the cost of a coffee) and t (the cost of a tea)

\[\begin{align} 2c + t &= 5\\ 3c + 5t &= 11 \end{align}\]

which can be solved to show that a coffee costs £2 and a tea £1.

This can be seen graphically by plotting the two equations for the price of coffee and tea on the same graph.

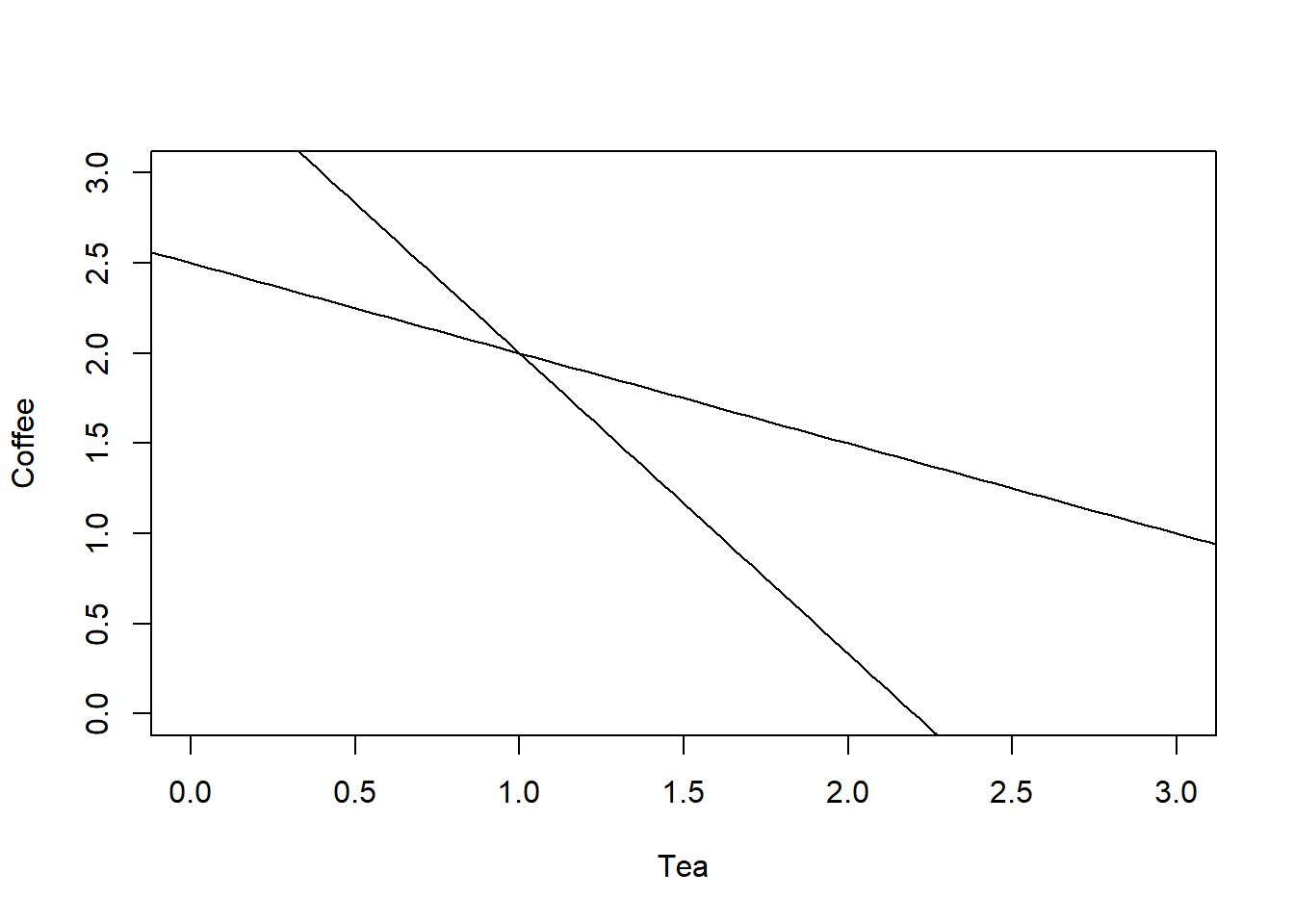
5.1 Linear equations

There are two methods which are generally used to solve simultaneous equations — elimination and substitution. The goal in both cases is to produce an equation with just one of the unknown variables.

5.1.1 Elimination

One of the fundamental rules of solving equations of any sort is that whatever you do to one side you must do to the other. The elimination method uses this by adding or subtracting equations — since, by definition, both sides of an equation are equal, when we add or subtract one equation from a second equation, we are adding or subtracting the same thing from both sides, even it it doesn’t look like that.

E.g. adding \(x + 3y = 8\) to \(x + y = 6\) gives \(2x + 4y = 14\)

The example is perfectly correct maths, but hasn’t helped us reach our goal of having an equation with just one unknown in it. However, if we subtract the second equation from the first, we get

\[\begin{align} & & x + 3y &= 8 \\ -\qquad & & x + y &= 6 \\ =\qquad & & 2y &= 2 \end{align}\]

We have now eliminated the x and have an equation just in y which can be solved giving \(y=1\). Having solved for y we can now substitute it into either equation to get x. In this case the second equation is easier — we get \(x + 1 = 6\) which means \(x = 5\).

This was a very straightforward example, as we only had one x in each equation. Most simultaneous equations are more complicated, for example:

\[\begin{align} 2x + 5y &= 15 \\ x + y &= 6 \end{align}\]

In this case we can eliminate x by multiplying the second equation by 2, giving us a new equation \(2x + 2y = 12\). The system of equations can then be solved the same way as before:

\[\begin{align} & & 2x + 5y &= 15 \\ -\qquad & & 2x + 2y &= 12 \\ =\qquad & & 3y &= 3 \end{align}\]

which again gives us \(y=1\) and \(x=5\).

Alternatively we could have chosen to eliminate y by multiplying the second equation by 5, giving us \(5x + 5y = 30\), leading to

\[\begin{align} & & 2x + 5y &= 15 \\ -\qquad & & 5x + 5y &= 30 \\ =\qquad & & -3x &= -15 \end{align}\]

which gives us \(x=5\) and then \(y=1\).

Most often you will need to multiply both equations to get a term you can eliminate.

E.g.

\[\begin{align} 2x + 5y &= 15 \\ 3x + 2y &= 17 \end{align}\]

  • Our first step is to decide which variable to eliminate — it doesn’t matter which. Let’s go for x here.

  • In the first equation the coefficient of x is 2 and in the second equation it is 3. The lowest common multiple of 2 and 32 is 6, so we would like to multiply the equations so the coefficient of x is 6 in each each equation. That means multiplying the first equation by 3, and the second by 2, giving us:

\[\begin{align} 6x + 15y &= 45 \\ 6x + 4y &= 34 \end{align}\]

  • This can now be solved as before:

\[\begin{align} & & 6x + 15y &= 45 \\ - \qquad & & 6x + 4y &= 34 \\ = \qquad & & 11y &= 11 \end{align}\]

giving us \(y=1\) and \(x=5\) as before.

In general the steps are:

  1. Rearrange both equations in the form \(ax + by = c\) if necessary.
  2. Write the equations one above the other.
  3. Decide which variable to eliminate.
  4. Find the lowest common multiple of the coefficients of that variable in the two equations.
  5. Multiply each equation to make the coefficients of the variable to be eliminated the same in each equation.
  6. Subtract one equation from the other to eliminate the variable.
  7. Solve the resulting equation for the remaining variable.
  8. Substitute the value just found back into one of the equations to solve for the eliminated variable.
  9. Put both values into the other equation to double check — this is not essential, but highly recommended!

5.1.2 Substitution

The other main method to solve simultaneous equations is to use one of the equations to find an expression for one variable, and then substitute it into the other equation.

E.g.

\[\begin{align} 2x + 5y &= 15 \\ x + y &= 6 \end{align}\]

Instead of subtracting the second equation from the first, we can solve it for x to give

\[x = 6 - y\]

This can then be substituted into the first equation and solved:

\[\begin{align} 2( 6 - y) + 5y &= 15 \\ 12 - 2y + 5y &= 15 \\ 12 +3y &= 15 \\ 3y &= 3 \\ y &= 1 \end{align}\]

as before.

There are fewer steps in this method than elimination, but the algebra can be more involved.

5.2 Linear and quadratic equations

The last section dealt with two linear simultaneous equations, and the two most common ways to solve them. Not all equations, however, are linear. Imagine trying to solve

\[\begin{align} y &= x + 1 \\ y &= x^2 -4x + 5 \end{align}\]

This can be examined graphically:

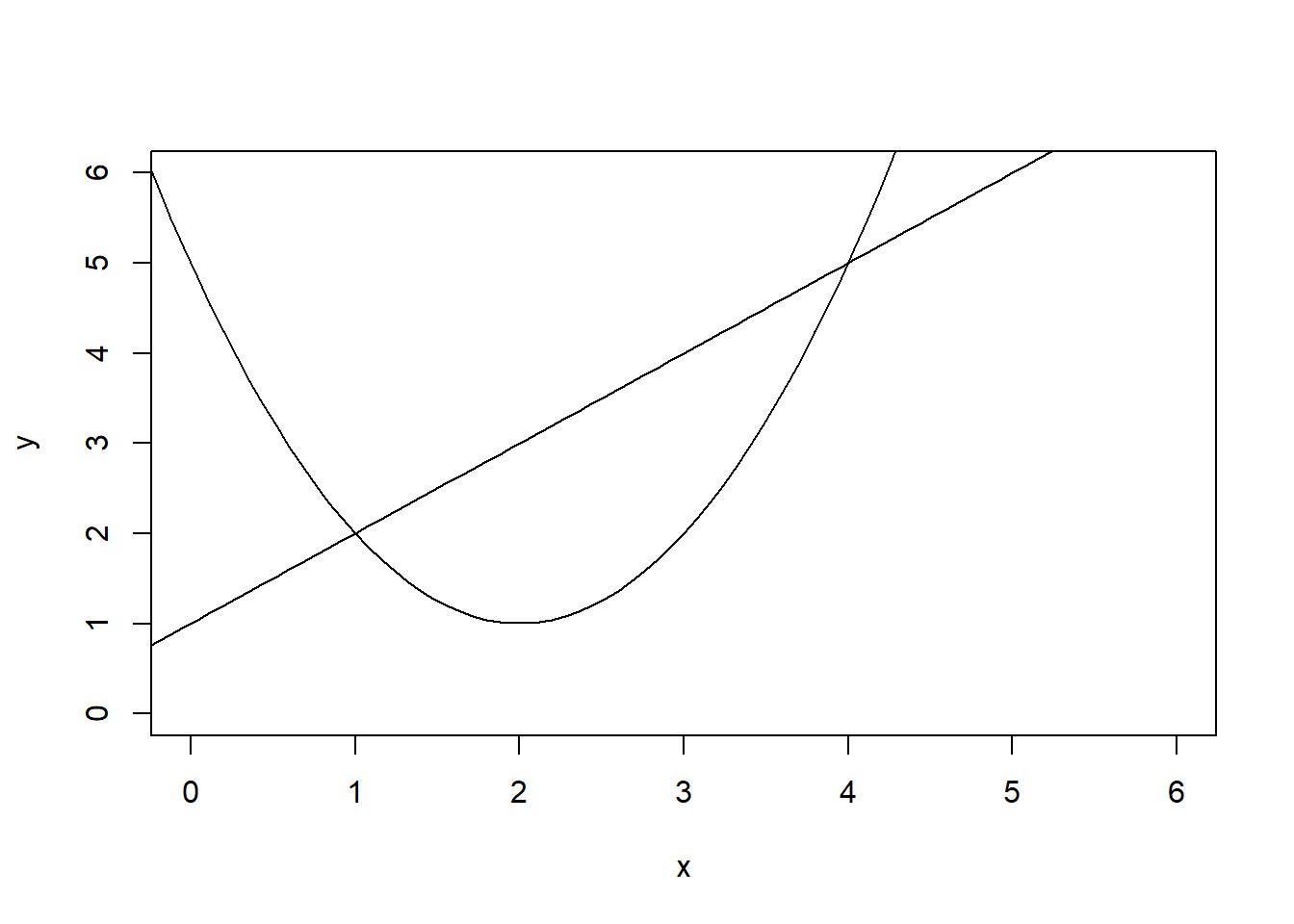
and it is clear that there are two solutions. The easiest way to solve is to use substitution. Substituting the linear equation into the quadratic, gives us:

\[ x + 1 = x^2 -4x + 5 \]

which can be solved in the same way as any quadratic equation:

\[\begin{align} x + 1 &= x^2 -4x + 5 \\ x^2 -5x +4 &= 0 \\ (x-1)(x-4) &= 0 \end{align}\]

which gives us \(x = 1\) and \(x = 4\). Substituting into the linear equation gives \(y = 2\) and \(y = 5\) respectively, so the solutions are: \((1,2)\) and \((4,5)\).

5.3 Linear equations and the equation of a circle

The last section looked at where a line and a parabola cross. Another common case is a line and a circle. E.g.

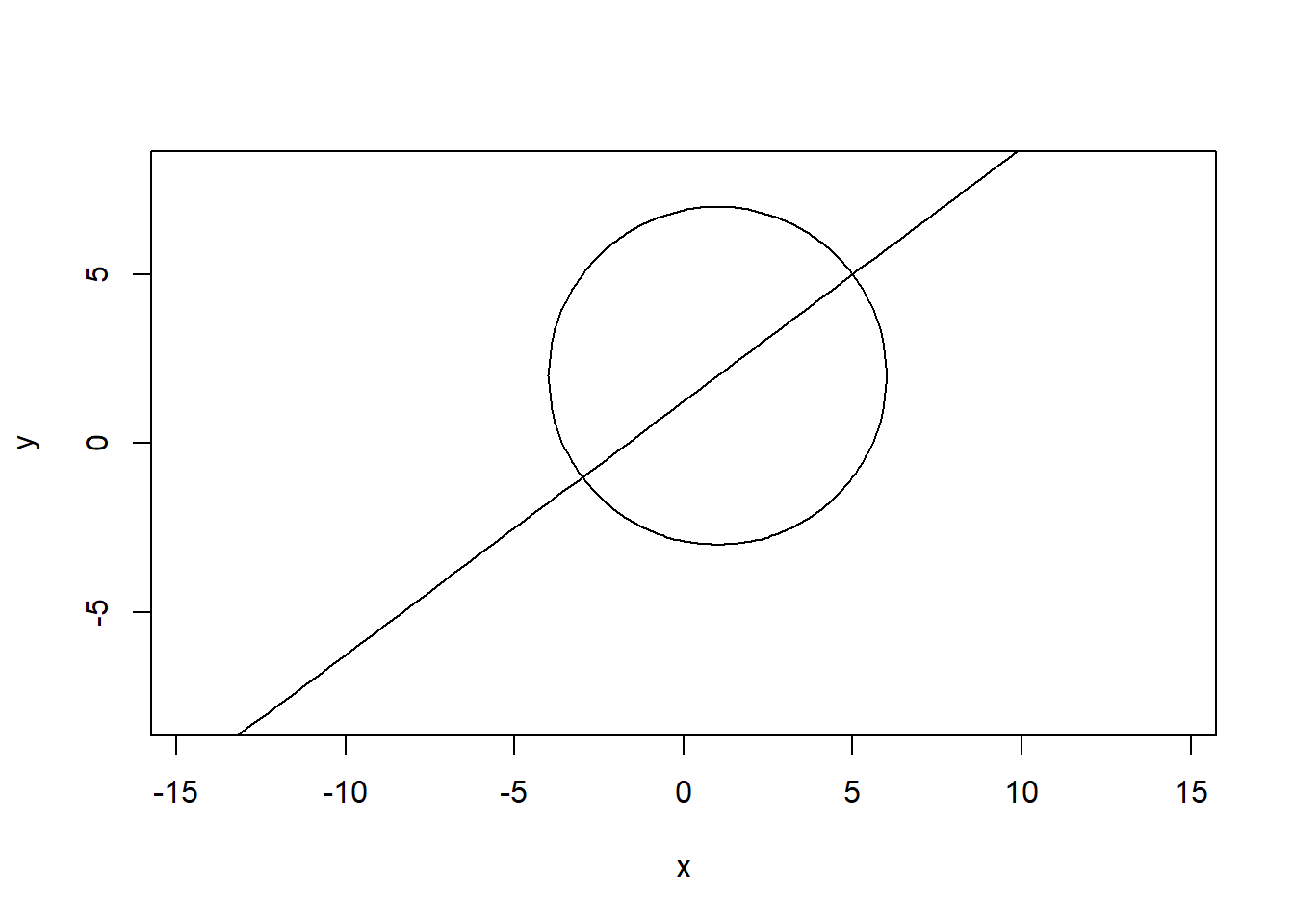\[\begin{align} 3x -4y +5 &= 0 \\ x^2 + y^2 -2x -4y &= 20 \end{align}\]

Just as in the quadratic equation case, the easiest way to tackle this is via substitution:

  1. Rearrange the linear equation to make y (or x — it doesn’t matter which) the subject \[ y = {(3x+5) \over 4} \]
  2. Substitute it into the second equation \[ x^2 + \left( {(3x+5) \over 4} \right)^2 -2x -4\left( {(3x+5) \over 4} \right) = 20\]
  3. Simplify \[ x^2 -2x -15 = 0\]
  4. Solve \[ x = -3\qquad \mathrm{or}\qquad x = 5\]
  5. Put the solutions for x back into the linear equation to get y, and thus the coordinates of the solutions \[ (-3, -1)\qquad \mathrm{and}\qquad (5,5)\]

  1. The smallest number which both numbers go into↩︎