Topic 4 Quadratic equations

A quadratic equation is something which looks like

\[3x^2+2x-4=0\]

I.e. the highest power of the unknown variable — x in this case — is $x^2$. A general quadratic has the form

\[\begin{equation} ax^2+bx+c=0\qquad a \ne 0 \tag{4.1} \end{equation}\]

where a,b and c are constants, and b or c could be equal to zero and so not appear. x is the unknown whose value (or values) need to be found.

In general there are two possible solutions to such equations, as can be seen by plotting

\[y=ax^2+bx+c\] and seeing where $y=0$. E.g.

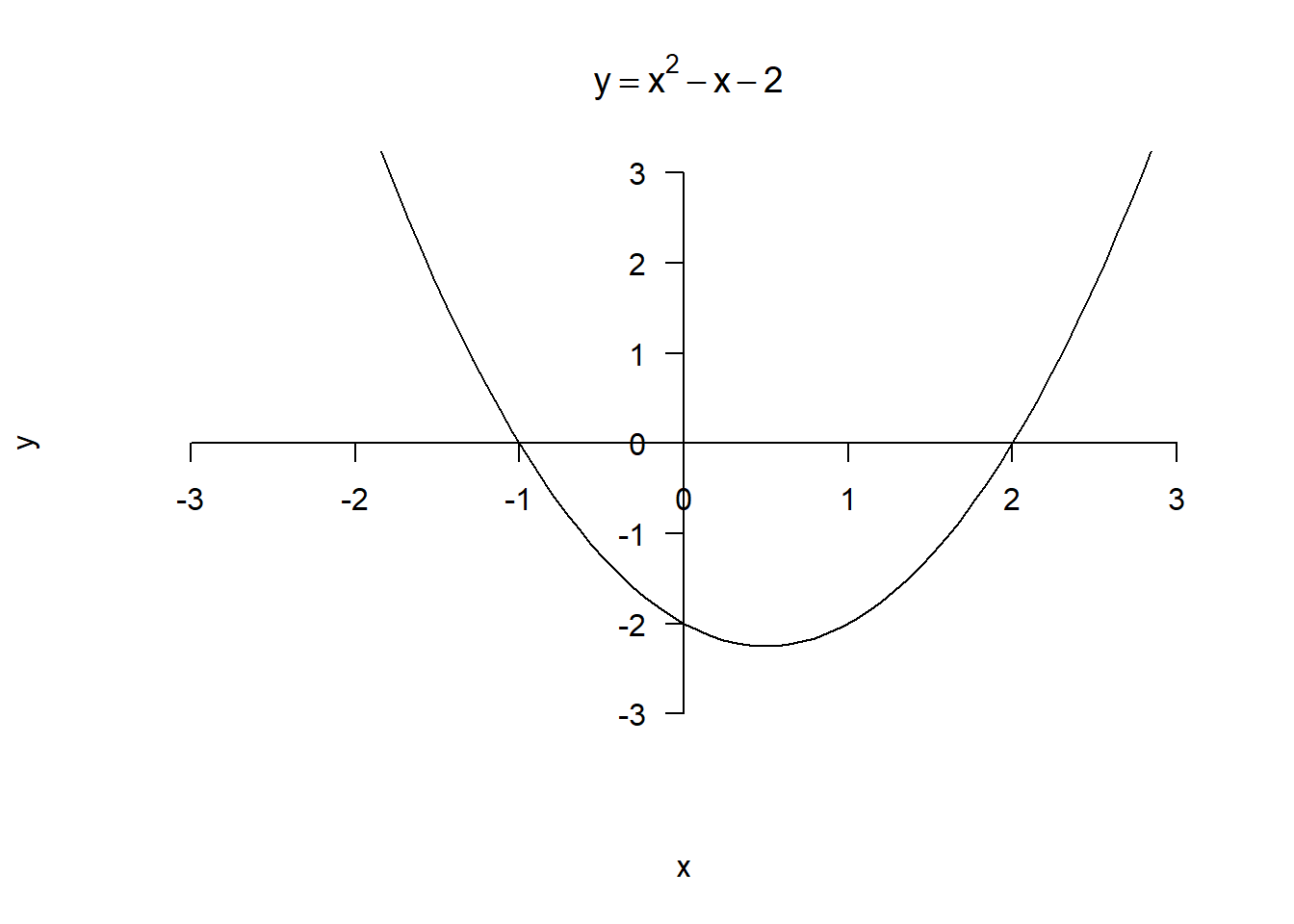
where we can see that $y=x^2-x-2$ crosses the x axis at $x=-1$ and $x=2$ so these are solutions to $x^2-x-2=0$.

Solving the equation graphically isn’t really a good option, and there are three methods which are generally used to solve it analytically.

Factorisation
Completing the square
The quadratic formula

4.1 Factorisation

Note that there are several methods of factorising quadratics, so the method I describe below may be slightly different from the one you know. There is no “one right way” — if you have a method which works for you, use it.

Before moving on to factorisation, it is worth examining expanding double brackets to form quadratic expressions.

You will have been taught at least one method to expand double brackets, e.g. “FOIL” (First Inner Outer Last) the other method which goes by many names, such as “crab claws.” These are very useful in practice, however I would like to go back to basics for the purposes of this section.

Suppose I want to expand $(2x+3)(4x-5)$ without using FOIL or crab claws. I could expand either bracket, e.g.

\[2x(4x-5) + 3(4x-5)\]

and then expand it again to get

\[\begin{equation} 8x^2 -10x +12x -15 \tag{4.2} \end{equation}\]

finally giving

\[8x^2+2x-15\]

I could have expanded it the other way, giving

\[4x(2x+3) -5(2x+3)\]

then

\[\begin{equation} 8x^2 + 12x -10x -15 \tag{4.3} \end{equation}\]

again giving

\[8x^2+2x-15\]

If you examine equation (4.2) and equation (4.3) you will see that they only differ in the order of the two middle terms. Many methods of factorisation hinge upon trying to find these two middle terms, and then factorising from there — basically doing the above expansion in reverse.

E.g. If I start with $8x^2+2x-15$ my steps are:

Split the middle term up so I have $8x^2+12x-10x-15$
Examine the first two terms $8x^2+12x$
- Identify $4x$ as a common factor
- Factorise to give $4x(2x+3)$
Examine the last two terms $-10x-15x$
- Identify $-5$ as a common factor
- Factorise to give $-5(2x+3)$
I now have $4x(2x+3) - 5(2x+3)$ which has a common factor of $(2x+3)$
- I can now factorise that out to give me $(2x+3)(4x-5)$

The first step is the hardest — finding the way to split up the middle term (the term in x). The trick is to look for two numbers that 1. Add to give the coefficient of $x$ (b in the general equation, $+2$ in this example) 2. Multiply together to give the product of the coefficient of $x^2$ (a in the general equation, $+8$ in this example), with the constant term (c in the general equation, $-15$ in this example).

E.g. we were looking for two numbers which add to give $+2$ and multiply to give $8*(-15) = -120$

We know that one is positive and one negative, otherwise the product would be positive
We can use (educated) guesswork, or do it systematically by looking at factors of $-120$
- 1 and -120 add to give -119
- 2 and -60 add to give -58
- 3 and -40 add to give -37
- 4 and -30 add to give -26
- 5 and -24 add to give -19
- 6 and -20 add to give -14
- 8 and -15 add to give -7
- 10 and -12 add to give -2
Since 10 and -12 add to give -2, -10 and 12 add to give 2 which is what we are looking for, hence the middle term $2x$ can be split into $12x-10x$.

4.2 Roots

Often factorisation is the goal — for instance when quadratics appear in the denominators of fractions.

However, we often want to find the solutions to $ax^2+bx+c=0$, which are also called the roots of the quadratic, and are the x-coordinates of the points where $y=ax^2+bx+c$ crosses (or touches) the x axis.

Once we have factorised it, we get something of the form

\[\begin{equation} (px+q)(rx+s)=0 \tag{4.4} \end{equation}\]

It is a general rule that if two (or more) numbers multiply to give 0 then at least one of them must be equal to 0 itself. This means that we can make equation @ref(eq:quad-factorised}) true by setting either of the two bracketed expressions equal to zero, giving us the two equations:

\[\begin{align} px+q &=0 \\ \mathrm{or} \qquad rx+s &=0 \end{align}\]

which lead to the two possible solutions:

\[\begin{align} x &= -{q \over p} \\ \mathrm{and} \qquad x &= -{s \over r} \end{align}\]

So in our example of $8x^2+2x-15$ we factorised to get $(2x+3)(4x-5)$. Thus the solution to $8x^2+2x-15 = 0$ is the same as the solution of $(2x+3)(4x-5) = 0$ and is given by the two possibilities:

\[\begin{align} 2x+3 &=0 \\ \mathrm{or} \qquad 4x-5 &=0 \end{align}\]

which gives us:

\[\begin{align} x &= -{3 \over 2} \\ \mathrm{and} \qquad x &= {5 \over 4} \end{align}\]

4.2.1 Easy case 1: $b = 0$

The previous section outlined the general case of (4.1)

\[\begin{equation} ax^2+bx+c=0\qquad a \ne 0 \end{equation}\]

There are, however, a couple of cases where the equation can be solved quickly without having to worry about factorisation, or the techniques described later. This is when either $b=0$ or $c=0$.

When $b=0$ the equation looks like

\[ax^2 + c = 0\] This can easily be rearranged to give \[ax^2 = -c\] and hence \[ x = \pm \sqrt{- c\over a}\]

For example, if $3x^2 - 2x = 0$, $x = \sqrt{2 \over 3}$ or $x = -\sqrt{2 \over 3}$.

4.2.2 Easy case 2: $c = 0$

The other easy case is when $c = 0$, i.e. we have an equation like

\[ax^2 + bx = 0\] Since both terms have a common factor of x this can be factorised to give

\[x(ax + b) = 0\] and, as we have two numbers multiplying to give zero, we get the two possibilities:

\[\begin{align} x &=0 \\ \mathrm{or} \qquad ax+b &=0 \end{align}\]

which gives us:

\[\begin{align} x &= 0 \\ \mathrm{and} \qquad x &= -{b \over a} \end{align}\]

as solutions.

For example, if $2x^2 + 3x = 0$, we get $x=0$ and $x = -{3\over 2}$

4.3 Completing the square

The next technique for dealing with quadratics is based around turning the expression into a perfect square with something left over. In arithmetic a perfect square is a number made up of squaring a whole number, e.g. 4,9,16,15,… In algebra we can do a similar thing:

\[(a+b)^2 = a^2 + 2ab + b^2\]

so we can think of $a^2 + 2ab + b^2$ as a perfect square, as it is the square of $(a+b)$.

When dealing with quadratics, we are interested in terms like $(x+p)^2$

\[\begin{equation} (x+a)^2 = x^2 + 2px + p^2 \tag{4.5} \end{equation}\]

E.g.

\[(x+3)^2 = x^2 + 6x + 9\]

\[(x+5)^2 = x^2 + 10x + 25\] \[(x-5)^2 = x^2 - 10x + 25\]

The important thing to notice here is that the coefficient of x is always twice p in a perfect square. This means that if I see an expression like $x^2+10x$ I know that $p = 5$ it must be related to the perfect square $(x+5)^2$:

\[\begin{align} x^2 + 10x &= x^2 + 10x + 25 - 25\\ &= (x+5)^2 - 25 \end{align}\]

The first step is allowed as $25-25=0$ so hasn’t changed the equation. By adding and subtracting 25 from this equation we have been able to “complete the square.” The 25 was chosen as it is $5^2$, or $p^2$ in the general case — see equation (4.5).

E.g. If we want to complete the square on $x^2+8x$ we:

Look at the coefficient of x, which is 8
Halve it to get $p = 4$
Square p to get 16
Then add and subtract the 16 from the equation \[ x^2 + 8x = x^2 + 8x + 16 - 16\]
Then rewrite the first three terms as a perfect square; giving us \[ x^2 + 8x = (x+4)^2 - 16\]

So far we have looked at completing the square where the p term in equation (4.5) is an even number. This is rarely the case, but the same principle applies:

E.g. If we want to complete the square on $x^2+7x$ we:

Look at the coefficient of x, which is 7
Halve it to get $p = \frac{7}{2}$
Square p to get $\frac{49}{4}$
Then add and subtract the $\frac{49}{4}$ from the equation \[ x^2 + 8x = x^2 + 7x + \frac{49}{4} - \frac{49}{4}\]
Then rewrite the first three terms as a perfect square; giving us \[ x^2 + 8x = \left(x+\frac{7}{2}\right)^2 - \frac{49}{4}\]

This is the basic technique of completing the square, however you won’t often see $x^2 + bx$ by itself. You will often see $x^2 + bx + c$, e.g. $x^2 + 4x + 5$. The trick here is to ignore the last number and just concentrate on the $x^2 + 4x$ term, which you know how to complete the square on.

E.g.

\[\begin{align} x^2 + 4x + 5 &= (x^2 + 4x) + 5\\ &= (x^2 + 4x + 16 - 16) + 5\\ &= [(x+2)^2 -16] +5\\ &= (x+2)^2 - 16 + 5\\ &= (x+2)^2 - 11 \end{align}\]

Where only the last step involved the c term.

You will remember that the general quadratic is given by $ax^2 + bx + c$. So far we have only looked at cases where $a=1$. Just as when $ c $ we can easily reduce the general case to what we have studied before, by factorising out the a, the continuing as before:

E.g. If we want to complete the square on $2x^2 + 8x + 5$, we:

Ignore the last term as before \[2x^2 + 6x + 5 = [2x^2 + 8x] + 5\]
Factorise out the coefficient of $x^2$ (the a term) \[2x^2 + 6x + 5 = 2[x^2 + 4x] + 5\]
Complete the square inside the brackets \[2x^2 + 6x + 5 = 2[(x+2)^2 -4] + 5\]
Multiply out the outer bracket \[2x^2 + 6x + 5 = 2(x+2)^2 - 8 + 5\]
Combine the last two terms \[2x^2 + 6x + 5 = 2(x+2)^2 -3\]

4.3.1 Using completing the square to solve quadratic equations

If we are given $ax^2+bx+c=0$ we can use completing the square to find the solutions (also called roots).

E.g. If we have $x^2 + 6x + 5 = 0$, we can:

Complete the square on the left hand side, giving us: \[(x+3)^2 - 4 = 0\]
Add 4 to both sides to get: \[(x+3)^2= 4\]
Square root both sides: \[(x+3) = \pm 2\]
Subtract 3 from both sides: \[ x = -3 \pm 2\]
Which gives us $x = -3 + 2$ and $x = -3 - 2$
So $x=-1$ and $x=-5$ are the solutions.

Note that if, in the last example, the right hand side on step 2 had been negative, there wouldn’t be a solution.

4.4 The quadratic formula

If you are just interested in solving equation (4.1)

\[\begin{equation} ax^2+bx+c=0\qquad a \ne 0 \end{equation}\]

then factorisation or completing the square may be more work than you’d like to do. In this case there is a simple formula for the roots (solutions to the equation)

\[\begin{equation} x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \tag{4.6} \end{equation}\]

E.g. If I want the roots of $3x^2 + 9x + 4$, I would:

Identify $a=3$, $b=9$, $c=4$
Use the formula: \[\begin{align} x &= \frac{-9 \pm \sqrt{9^2 - 4 \times 3 \times 4}}{2 \times 3}\\ &= \frac{-9 \pm \sqrt{81 - 48}}{6}\\ &= \frac{-9 \pm \sqrt{33}}{6} \end{align}\]
Giving the roots as: $x=\frac{-9 + \sqrt{33}}{6}$ and $x=\frac{-9 - \sqrt{33}}{6}$.

Where people generally get into trouble is when one or more of the coefficients (a, b or c) are negative. The trick, as ever with negative numbers, is to use brackets.

E.g. If I want the roots of $3x^2 - 9x - 4$, I would:

Identify $a=3$, $b=-9$, $c=-4$
Note that b and c are negative
Use the formula, making sure I bracket all cases of b and c: \[\begin{align} x &= \frac{-(-9) \pm \sqrt{9^2 - 4 \times 3 \times (-4)}}{2 \times 3}\\ &= \frac{9 \pm \sqrt{81 + 48}}{6}\\ &= \frac{9 \pm \sqrt{129}}{6} \end{align}\]
Giving the roots as: $x=\frac{9 + \sqrt{129}}{6}$ and $x=\frac{9 - \sqrt{129}}{6}$.

4.4.1 Number of roots and the discriminant

Look back at the quadratic formula

\[\begin{equation} x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{equation}\]

The expression in the square root $b^2 - 4ac$ is very important, and is called the discriminant.

If it is negative, there is no solution to the equation (no roots)
If it is zero, the two roots are the same.
If it is greater than zero, there are two distinct solutions.

E.g. How many solutions are there to $3x^2+2x+5 = 0$? * $a=3$,$b=2$,$c=5$ * The discriminant is $b^2 - 4ac = 2^2-4\times 3 \times 5$ so the discriminant is -56. * This is negative, so there are no solutions.

E.g. How many solutions are there to $3x^2+2x-5 = 0$? * $a=3$,$b=2$,$c=-5$ * The discriminant is $b^2 - 4ac = 2^2-4\times 3 \times (-5)$ so the discriminant is 64. * This is positive, so there are two solutions.

LJMU Maths Refresher