Topic 6 Inequalities
If I showed you a box and asked you how many apples are in it, you probably wouldn’t be able to give me an exact answer, but you might be able to say “less than 30.” If I asked how long a ladder would need to be to climb over a fence, you could say “2 metres long,” but a longer ladder would also work, so you could also say “at least 2 metres long.” These are examples of inequalities; they express the range of values which would be acceptable, by specifying the ends of those ranges. There are five mathematical symbols to describe inequalities:
- Less than — the left hand number could be every number up to, but not including, the right hand number
- “x is less than 6” becomes
- is true
- isn’t true
- isn’t true
- Greater than — the right hand number could be every number up to, but not including, the left hand number
- “x is greater than 5” becomes
- is true
- isn’t true
- isn’t true
- Less than or equal to — the left hand number could be every number up to, and including, the right hand number
- “x is less than or equal to 6” becomes
- is true
- isn’t true
- is true
- Greater than or equal to — the right hand number could be every number up to, and including, the left hand number
- “x is greater than or equal to 5” becomes
- is true
- isn’t true
- is true
- Not equal to — the two numbers are different
- “x is not equal to 5” becomes
- is true
- isn’t true
“” and “” are referred to as strict inequalities, as they do not include the endpoints, so you could say, for instance, that “x is strictly less than 6” for .
An inequality can also be used to express a range. E.g. suppose we have and , this could be written as one inequality
6.1 Linear inequalities
Suppose I want to know the set of values of for which
I can treat this just as I would any equation, i.e. subtract 3 from both sides and get
Similarly for subtraction. In general you can treat an inequality just like you would any equation, with one proviso — if you multiply or divide by a negative number you must swap the direction of the inequality. To illustrate why, consider
If I multiple both sides by I get 5 on the left, and 1 on the right, and we know that
Similarly, if I have
I must have
6.2 Quadratic inequalities
Now consider . If this were an equation rather than an inequality, i.e. we had , we could factorise it to give and solve to get and . However we have an inequality. Let’s look at the graph of :
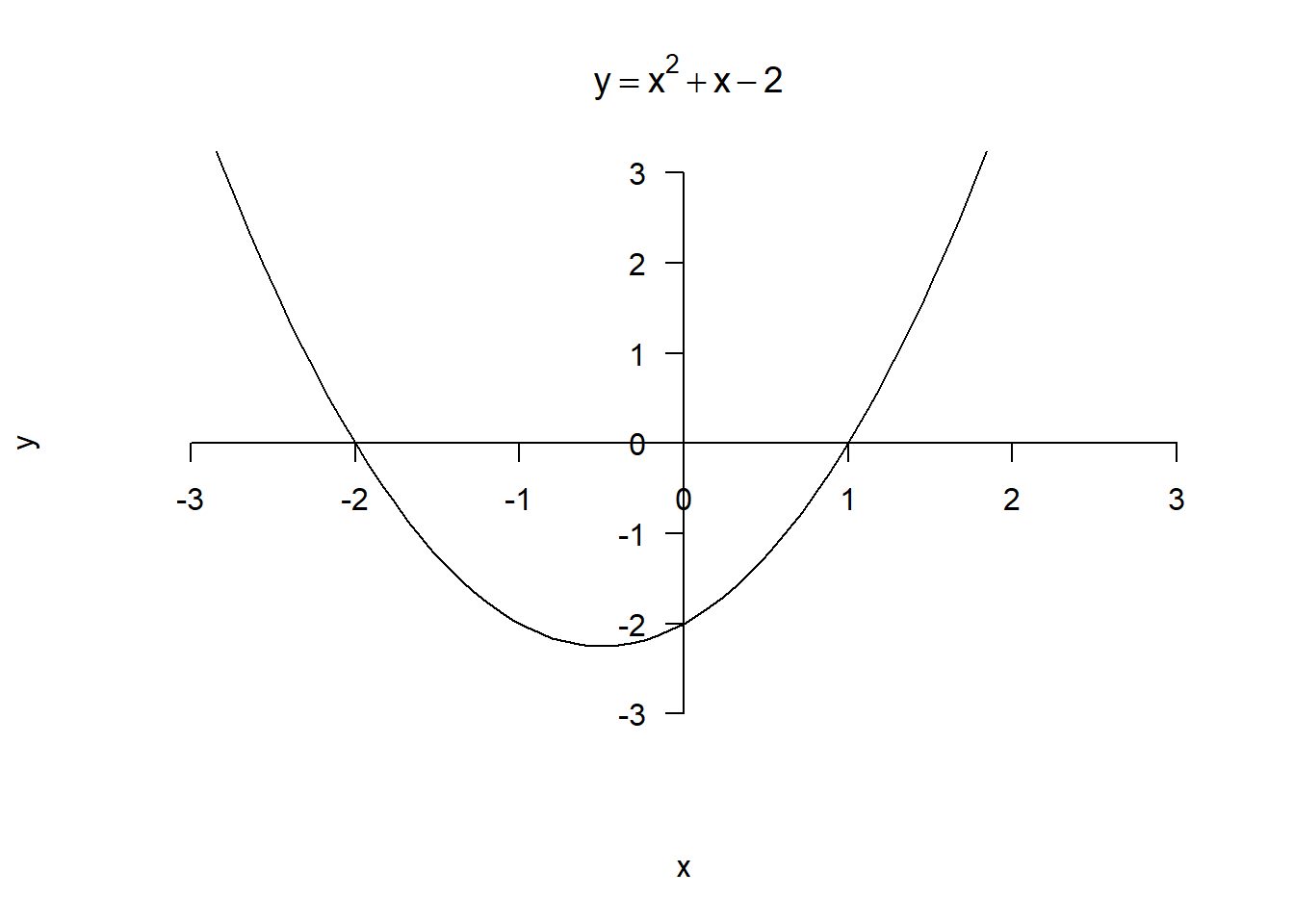
We are interested in when , which is clearly when
Similarly if we had been interested in we would look at where and get
as the solution.
So, in general for a quadratic inequality:
- Find the roots of the corresponding equality
- Do a quick sketch of the graph
- Inspect the graph to see which region solves the inequality.