Topic 2 Percentages
2.1 What is a percentage
A percentage is another way of presenting a fraction. It literally means “per 100,” and so when you express a number as a percentage it means writing it as a number out of 100.
2.2 Writing one number as a percentage of another
In order to calculate what percentage you have, divide the two numbers and multiply by 100.
E.g. If I have 25 apples and 5 of them are red, what percentage of the apples are red?
\[ \frac{5}{25} \times 100 = 20\%\]
If I have 4 cats and 3 dogs, I have a total of 7 animals.
\[ \frac{4}{7} \times 100 = 57\%\]
are cats, and
\[ \frac{3}{7} \times 100 = 43\%\]
are dogs.
We are not restricted to just two categories, and the above calculations are easily extended. If you have lots of categories the results are often shown in tables or bar graphs.
E.g.
| Pet | Count | Percentage |
|---|---|---|
| cat | 4 | 25.00 |
| dog | 3 | 18.75 |
| rabbit | 2 | 12.50 |
| parakeet | 7 | 43.75 |
| Total | 16 | 100.00 |
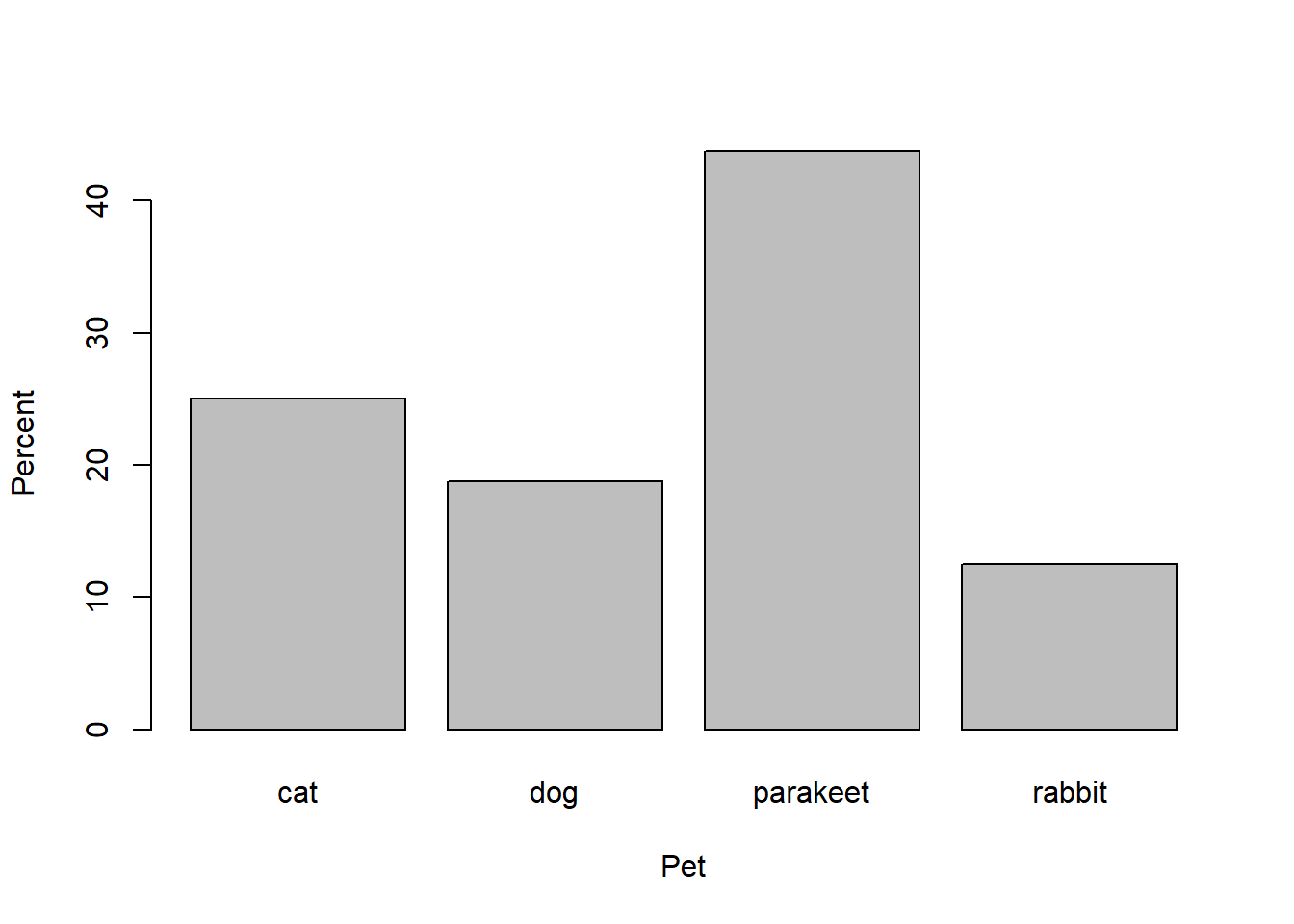
2.3 Percentage of an amount
If I have 16 pets and 25% of them are cats, I might want to know how many cats I have. Since 25% means 25 out of every 100, I can work this out with
\[ 16 \times \frac{25}{100} = 4 \]
2.4 Percentage increase and decrease
Prices rise and prices fall, and these are often expressed as percentages. If a hat costing £20 increases by 5%, I would like to know the new price. The easiest way to do this is to think that the price is now 105% of the old price, so I can work it out by doing the same calculation as in the last section.
\[ £20 \times \frac{105}{100} = £21 \]
Similarly if the hat is in a sale and has 20% off, the new prices is only \(100-20=80\)% of the old price, so I can do
\[ £20 \times \frac{80}{100} = £16 \]
2.5 Multipliers
By now you should be happy about the idea that a percentage is something out of a hundred, so 5% means 5 out of a 100, 80 percent means 80 out of a hundred. We have used this in the calculation by writing things like \(\frac{80}{100}\) explicitly in our calculations. We could, however, work that out first \(\frac{80}{100} = 0.8\) and just multiply by that first. E.g. 80% of £20 can be calculated as
\[ £20 \times 0.8 = £16 \]
This number, 0.8 here, is referred to as a multiplier and can save you a lot of time in calculations as long as you are happy about dividing numbers by 100.
E.g. If the price of apples was £2 per bag and it increases by 10% I now have 110%, which is a multiplier of 1.1. I can then calculate
\[ £2 \times 1.1 = £2.20 \]
to find the new price of a bag of apples.
2.6 Finding the original amount
Sometimes it is useful to know how much something was before a percentage increase or decrease happened. E.g. in the hat example from the last section, if I know the hat is now £16 and this is in a 20% sale, I might be interested in what the price was before the sale. This isn’t as simple as just adding 20% to the sale price, as this will be too small.
This is where being able to use multipliers, as described above, is really useful. In order to find the original amount, we just divide by the multiplier.
E.g. After a 10% increase in price a bag of apples now costs £2.20, what was the original price?
- Find the multiplier: 10% increase means we have 110% of the original amount. This is a multiplier of 1.1.
- Divide the new amount by the multiplier to get the original amount:
\[ \frac{£2.20}{1.1} = £2 \]